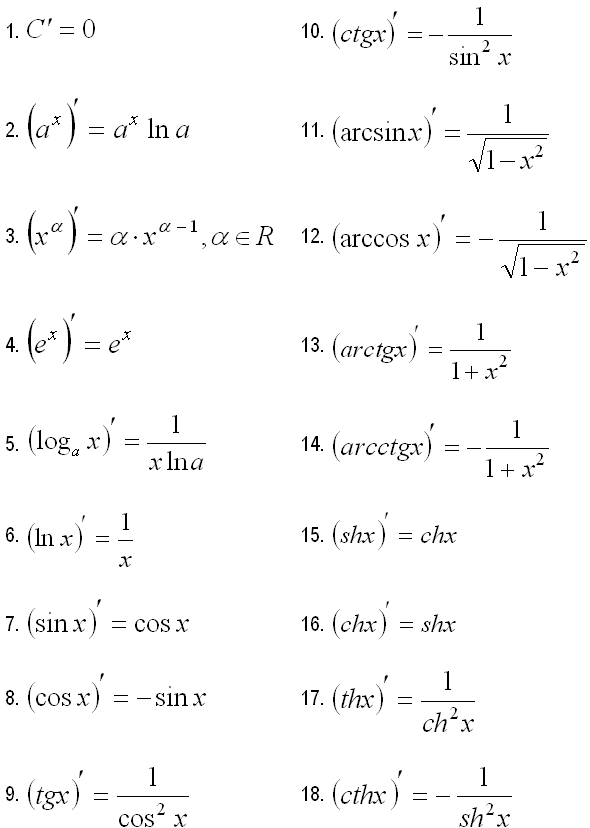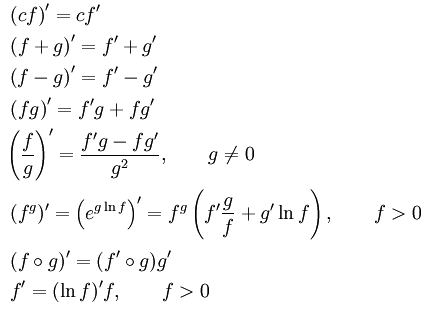 Пусть
Пусть 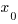 и и 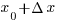 — значения аргумента, а — значения аргумента, а 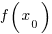 и и 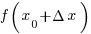 — соответствующие значения функции — соответствующие значения функции 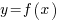 в этих точках. Тогда в этих точках. Тогда 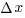 называется приращением аргумента, а разность называется приращением аргумента, а разность 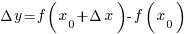 — приращением функции на отрезке [ — приращением функции на отрезке [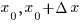 ]. ].
Производной функции 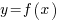 в точке в точке 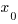 называется предел отношения приращения функции к приращению аргумента, когда называется предел отношения приращения функции к приращению аргумента, когда 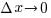 : :
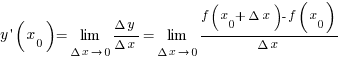 . .
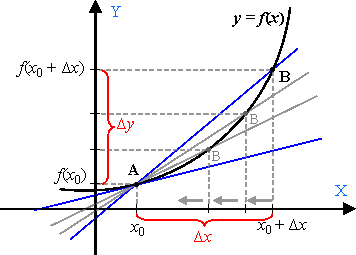
Геометрический смысл производной. Геометрически производная представляет собой угловой коэффициент касательной к графику функции 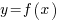 в точке в точке 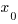 , т.е. , т.е. 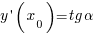 . .
Производная есть скорость изменения функции в точке 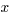 . Отыскание производной называется дифференцированием фукнции. . Отыскание производной называется дифференцированием фукнции.
Таблица производных
Зная таблицу производных и правила дифференцирования, вы сможете найти производную любой элементарной функции. Наша таблица производных имеет всего 18 формул, поэтому настоятельно рекомендуем выучить ее наизусть. Тогда задачи в которых необходимо найти производную функции вы сможете решить без проблем.
Правила дифференцирования общих функций
Вычисление производной — важнейшая операция в дифференциальном исчислении.
В этих формулах f и g — произвольные дифференцируемые функции вещественной переменной, а c — вещественная константа. Этих формул достаточно для дифференцирования любой элементарной функции.
Смотрите также Таблицу интегралов
Оцените по пятибальной шкале, как вам эта таблица производных?
Рейтинг: 2.8/5 (Всего оценок: 210)
|
 Пусть
Пусть 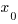 и
и 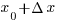 — значения аргумента, а
— значения аргумента, а 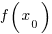 и
и 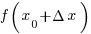 — соответствующие значения функции
— соответствующие значения функции 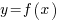 в этих точках. Тогда
в этих точках. Тогда 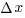 называется приращением аргумента, а разность
называется приращением аргумента, а разность 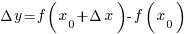 — приращением функции на отрезке [
— приращением функции на отрезке [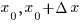 ].
].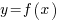 в точке
в точке 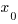 называется предел отношения приращения функции к приращению аргумента, когда
называется предел отношения приращения функции к приращению аргумента, когда 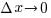 :
: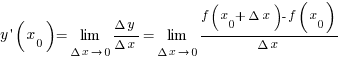 .
.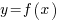 в точке
в точке 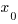 , т.е.
, т.е. 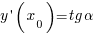 .
.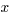 . Отыскание производной называется дифференцированием фукнции.
. Отыскание производной называется дифференцированием фукнции.