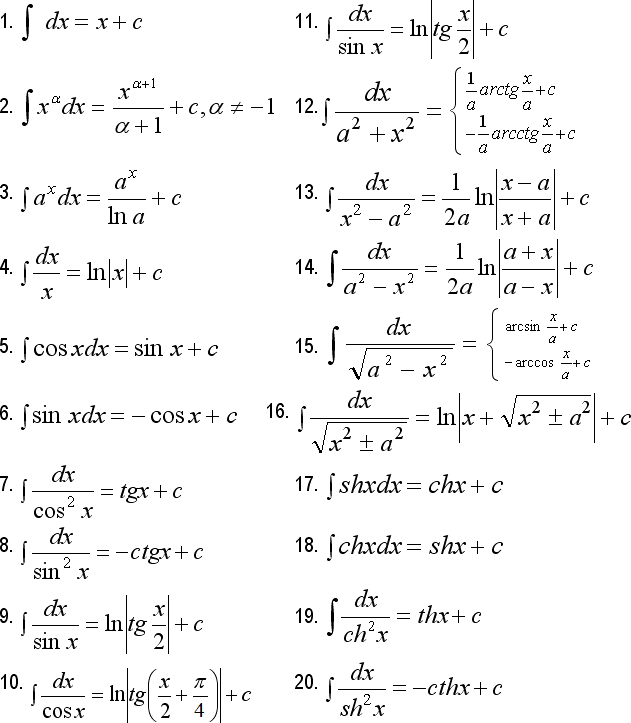|
5 класс:
6 класс:
7 класс:
8 класс:
Таблицы:
Популярные разделы:
Полезные материалы:
|
Таблица основных интегралов На этой странице представлена таблица интегралов. Большинство интегралов, с которыми встречаются школьники и студенты, сводятся к основным интегралам. Поэтому таблицу основных интегралов необходимо выучить наизусть. Также обязательно помнить таблицу производных.Ниже таблицы интегралов приведены свойства неопределенного интеграла. Применяя основные методы интегрирования, такие как подведения функции под знак дифференциала, замена переменной, или интегрирование по частям вы сможете свести ваш интеграл к табличному.
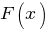 называется первообразной для функции называется первообразной для функции 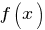 , если , если 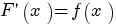 или или 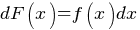 . .Если функция 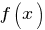 имеет первообразную имеет первообразную 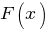 , то она имеет бесконечное множество первообразных, причем все первообразные содержатся в выражении , то она имеет бесконечное множество первообразных, причем все первообразные содержатся в выражении 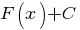 , где , где 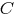 - постоянная. - постоянная.Неопределенным интегралом от функции 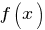 (или от выражения (или от выражения 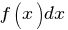 ) называется совокупность всех ее первообразных. Обозначение: ) называется совокупность всех ее первообразных. Обозначение: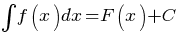 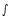 - знак интеграла, - знак интеграла, 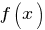 - подынтегральная функция, - подынтегральная функция, 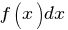 - подынтегральное выражение, - подынтегральное выражение, 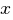 - переменная интегрирования. - переменная интегрирования.Отыскание неопределенного интеграла называется интегрированием функции. Свойства неопределенного интеграла 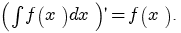 2. 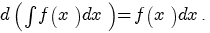 3. 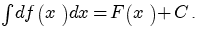 4. 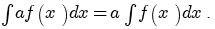 5. 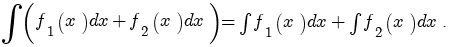 6. Если 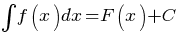 и и 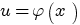 , то , то 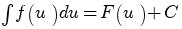
Смотрите также Таблицу производных
|
||||||||||||||||||||||||||
| © 2006-2021 Math.com.ua |
|
|