|
5 класс:
6 класс:
7 класс:
8 класс:
Таблицы:
Популярные разделы:
Полезные материалы:
|
Тригонометрические функции
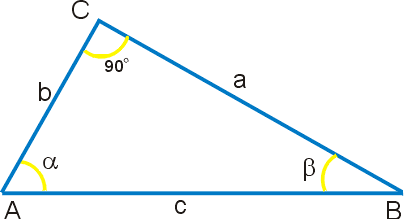
Тригонометрические функции в прямоугольном треугольнике
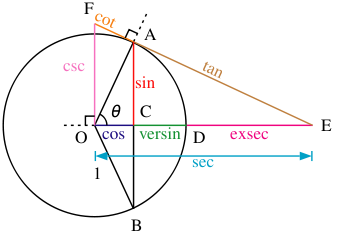
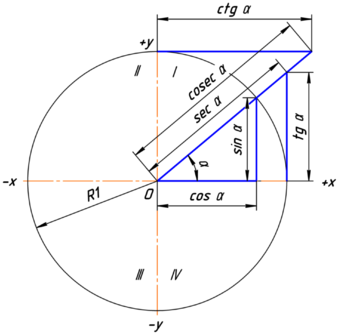
Определение тригонометрических функций через окружность
Определение тригонометрических функций через ряды
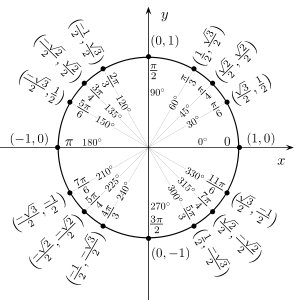
Значения тригонометрических функций для некоторых углов
Поставьте свою оценку:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| © 2006-2021 Math.com.ua |
|
|

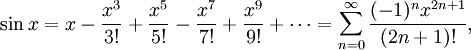
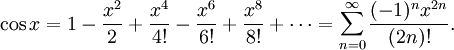
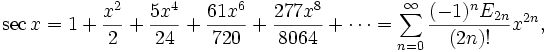 где En — числа Эйлера.
где En — числа Эйлера.