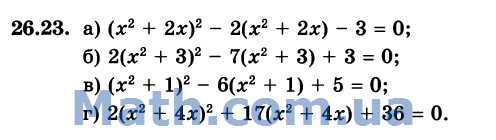Задача №26.23
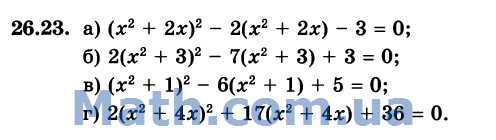
а) (X2 + 2л:)2 - 2(х2 + 2х) -3 = 0;
б) 2(х2 + З)2 - 7(х2 + 3) + 3 = 0;
в) (X2 + I)2 - 6(х2 + 1) + 5 = 0;
г) 2(х2 + 4х)2 + 17(*2 + 4х) + 36 = 0.
Решение задачи №26.23:
К сожалению, решение этой задачи на данный момент недоступно 126.23.1 а) (х2 + 2х)2 — 2 • (х2 + 2х) — 3 = 0,г/ = х2 + + 2х => у2 - 2г/-3 = 0 => = 4 + 4 - 3 = 16 => у\ = ^±4 =
= 3,2/2 = ^ = — 1 => х2 + 2х — 3 = 0, х2 4- 2х 4- 1 = = 0 => ?> = 4 + 4 • 3 = 16, (х + I)2 = 0 => XI = = !
х2 = -1; х3 = -3;
б) 2 • (х2 + З)2 - 7 • (х2 + 3) + 3 = 0, у — х2 + 3 => 2у2 --7у + 3 = 0=> И = 49-4-2-3 = 25 = 52 => ух = ^ = 3, 3/2 = 5 => а:2 -4-3 = 3, х2 + 3 = 5 => х2 = —2,5 — нет корней, х = 0.
в) (х2 + I)2 - 6 • (х2 + 1) + 5 = О, у = х2 + 1=>у2-
— 6у + 5 = 0=>?> = 36-4-5 = 16 = 42^у1 = ^ =
— 5,2/2 = ^ = 1=>х2 + 1 = 5, х2 + 1 = 1=>- Х1>2 = ±2,
хз = 0;
г) 2-(х2+4х)2 + 17-(х2+4х)+36 = 0, у = х2+4х => 2у2+ + 17у + 36 = 0 => И = 289-4-2-36 = 1, ух = =1|±± = -4, У2 = ~14~1 — | => х2 + 4х + 4 = 0, х2 + 4х + | = 0 => (х + + 2)2 = 0, 2х+8х + 9 = 0 => х = -2; И = 64-4-2-9 < 0 -нет корней.
Оцените это ГДЗ:
Рейтинг: 1.4/5 (Всего оценок: 19)
Выбор задания:
|